Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- Recursion
- 프로그래머스
- 반효경교수님
- SQL
- Sort
- 그래프
- 재귀
- 매개변수 탐색
- 가중치없는그래프
- 이분탐색
- MySQL
- git
- domain model
- 알고리즘
- lcap
- 백트래킹
- Bruteforce
- microflow
- 해시맵
- 완전탐색
- 집합
- 자바
- 자료구조
- 스택
- Mendix
- 정렬
- 트리
- algorithm
- dfs
- 멘딕스
Archives
- Today
- Total
mondegreen
부분집합(Subset) 본문
반응형
멱집합(PowerSet)의 수 = 2^n
아래는 부분집합을 구하는 알고리즘 문제이다.
1) 부분집합 * 순열(중복 순열 아님)
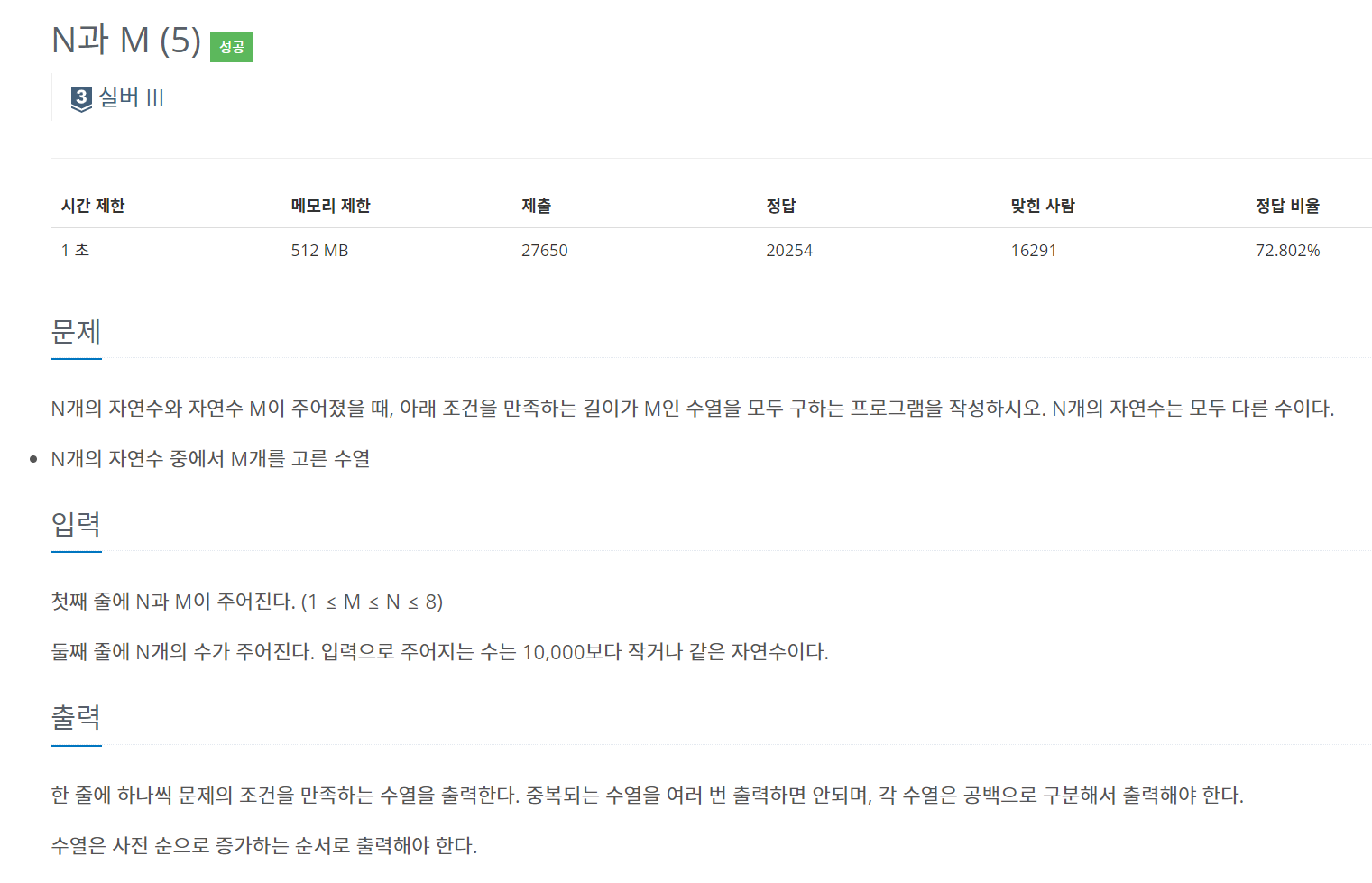
import java.util.Arrays;
import java.util.Scanner;
public class Main {
static int n, m;
static int[] arr, selected;
static boolean[] used;
static StringBuilder sb;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
arr = new int[n + 1];
selected = new int[m + 1];
int max = Integer.MIN_VALUE;
for (int a = 1; a <= n; a++) {
arr[a] = sc.nextInt();
max = Math.max(max, arr[a]);
}
used = new boolean[max + 1];
Arrays.sort(arr); // 정렬
sb = new StringBuilder();
rec(1);
System.out.println(sb.toString());
sc.close();
}
private static void rec(int idx) {
// 기저조건
if (idx == m + 1) {
for (int s = 1; s <= m; s++) {
sb.append(selected[s]).append(" ");
}
sb.append("\n");
return;
}
// 유도조건
for (int a = 1; a <= n; a++) {
if (used[arr[a]]) { // 중복 불허
continue;
// 직전에 뽑은 수와 대소비교 하지 않음으로써 순서 반영 -> 순열
}
selected[idx] = arr[a];
used[arr[a]] = true; // 방문처리
rec(idx + 1);
used[arr[a]] = false; // 방문처리 취소
}
}
}
2) 부분집합 * 조합(중복 조합 아님)
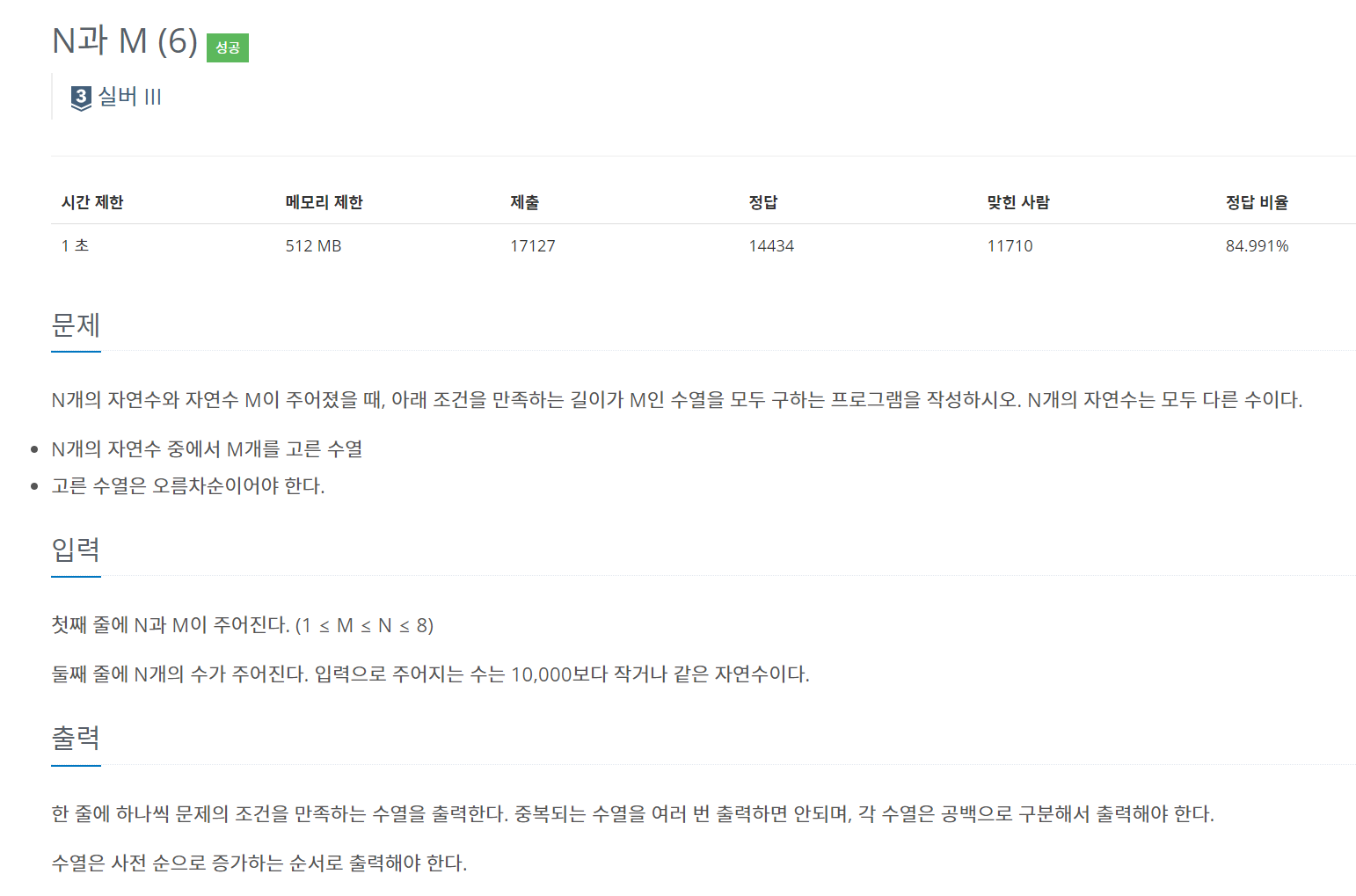
import java.util.Arrays;
import java.util.Scanner;
public class Main {
static int n, m;
static int[] arr, selected;
static StringBuilder sb;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
arr = new int[n + 1];
selected = new int[m + 1];
for (int a = 1; a <= n; a++) {
arr[a] = sc.nextInt();
}
Arrays.sort(arr); // 정렬
sb = new StringBuilder();
rec(1);
System.out.println(sb.toString());
sc.close();
}
private static void rec(int idx) {
// 기저 조건
if (idx == m + 1) {
for (int s = 1; s <= m; s++) {
sb.append(selected[s]).append(" ");
}
sb.append("\n");
return;
}
// 유도 조건
for (int a = 1; a <= n; a++) {
if (selected[idx - 1] < arr[a]) { // 직전의 수가 더 작은 경우에만
selected[idx] = arr[a]; // 수를 뽑는다 -> 조합
} else { // 크거나 같으면 뽑지 않는다. 그래야 순서 반영하지 않음
continue;
}
rec(idx + 1);
}
}
}반응형
'알고리즘 풀이 및 리뷰 > 알고리즘 이론' 카테고리의 다른 글
| 연결리스트(LinkedList) (0) | 2023.06.05 |
|---|---|
| 스택(Stack)과 큐(Queue) (0) | 2023.06.05 |
| 조합(Combination; 순서 X 중복 X) (0) | 2023.06.05 |
| 순열(Permutation; 순서 O 중복 X) (0) | 2023.06.05 |
| 완전검색(Brute Force, Generate and test) (0) | 2023.06.05 |


