| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- domain model
- Mendix
- 정렬
- 자바
- Recursion
- MySQL
- 집합
- 재귀
- 완전탐색
- 멘딕스
- 트리
- 그래프
- algorithm
- microflow
- 알고리즘
- lcap
- 반효경교수님
- 이분탐색
- 가중치없는그래프
- dfs
- git
- Bruteforce
- 해시맵
- 스택
- 매개변수 탐색
- SQL
- 프로그래머스
- Sort
- 자료구조
- 백트래킹
- Today
- Total
mondegreen
DFS(깊이 우선 탐색) 본문
깊이우선탐색의 개념
1) 루트 노드(또는 임의의 노드)에서 시작해 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법
2) 직전의 갈림선이 있는 정점을 되돌아가야 하기 때문에 재귀적으로 구현하거나, 후입선출 구조의 스택을 활용
; 시작 정점의 한 방향으로 갈 수 있는 가장 깊은 경로까지 탐색하다가 끝을 만나면 직전의 갈림선이 있는 정점으로 돌아와 다른 방향의 정점으로 탐색을 계속 반복하여 모든 정점을 탐색하는 방법
깊이우선탐색의 특징
1) 자기 자신을 호출하는 순환 알고리즘의 형태이다.
2) 위와 같은 이유로 방문한 노드는 그 여부를 반드시 검사해야 무한 루프에 빠지지 않는다.
3) 전위 순회, 중위 순회, 후위 순회 모든 형태의 트리 순회는 모두 DFS의 한 종류이다.
4) 인접 행렬 또는 인접 리스트로 표현할 수 있다.
5) BFS보다 구현이 간단하다.
6) 단순 검색 시, BFS에 비해 느리다.
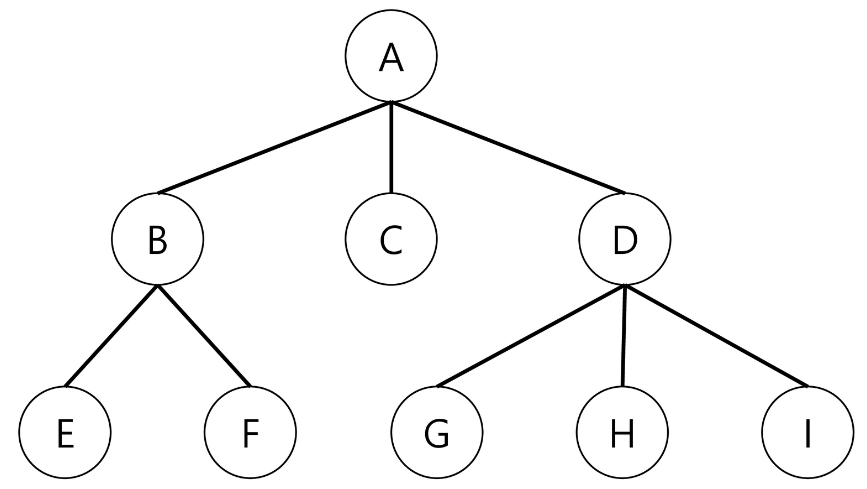
위와 같은 트리를 깊이 우선 탐색한다고 했을 때 구현 방법에 따른 노드별 탐색 순서가 다음과 같이 다르기 때문에
탐색 순서를 문제에서 지정한다면, 구현하는 방식을 달리 해야함을 유의
1) 재귀적으로 구현: A B E F C D G H I
2) STACK으로 구현: A D I H G C B F E
깊이 우선 탐색의 활용
모든 노드를 방문하고자 하는 경우이 이 방법을 선택한다.
깊이 우선 탐색의 시간 복잡도
DFS는 그래프(정점: N, 간선: E)의 모든 간선을 탐색한다.
1) 인접행렬로 구현 시: O(N^2)
2) 인접리스트로 구현 시: O(N+E)
백준 11724
import java.util.Scanner;
public class Main {
static int n, m, cnt;
static boolean[] visited;
static boolean[][] arr;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
visited = new boolean[n + 1];
arr = new boolean[n + 1][n + 1];
for (int i = 0; i < m; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
arr[a][b] = true;
arr[b][a] = true;
}
cnt = 0;
for (int i = 1; i <= n; i++) {
if (!visited[i]) {
cnt++;
visited[i] = true;
DFS(i);
}
}
System.out.println(cnt);
sc.close();
}
private static void DFS(int a) {
for (int j = 1; j <= n; j++) {
if (!visited[j]) { // 아직 확인되지 않았고
if (arr[a][j]) { // 둘은 연결되어 있다면...
visited[j] = true;
DFS(j);
}
}
}
}
}'알고리즘 풀이 및 리뷰 > 알고리즘 이론' 카테고리의 다른 글
| 최소 신장 트리(Minimum Spanning Tree)_크루스칼/프림 (0) | 2023.06.28 |
|---|---|
| 서로소 집합(Disjoint sets; 상호배타집합) (0) | 2023.06.27 |
| BFS(너비 우선 탐색) (0) | 2023.06.26 |
| 그래프 (0) | 2023.06.26 |
| 백트래킹 (0) | 2023.06.25 |


