| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Bruteforce
- algorithm
- 백트래킹
- 알고리즘
- git
- 자바
- domain model
- 가중치없는그래프
- 멘딕스
- Mendix
- 매개변수 탐색
- lcap
- dfs
- 자료구조
- 정렬
- 반효경교수님
- 집합
- 프로그래머스
- SQL
- 그래프
- 이분탐색
- Recursion
- Sort
- 스택
- 해시맵
- 완전탐색
- 트리
- MySQL
- 재귀
- microflow
- Today
- Total
mondegreen
[240217] 알고리즘 리부트 9일차 - 백준 3085 자바 본문
[240217] 알고리즘 리부트 9일차 - 백준 3085 자바
앙갱 2024. 2. 17. 22:56[Part1-Chapter04-Clip05]
- 백준 3085 사탕게임
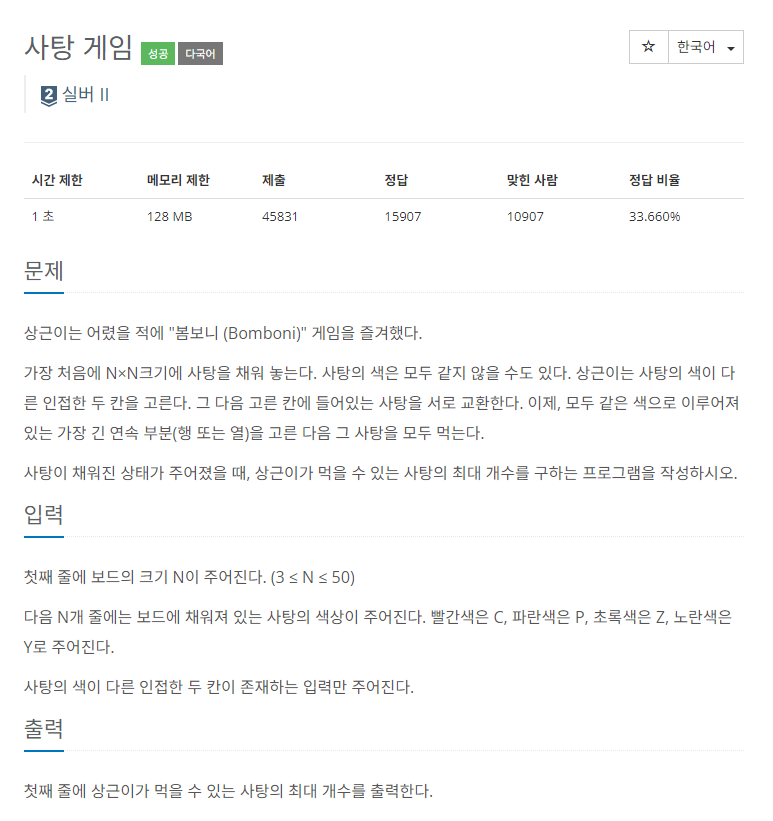
시간이 많이 걸린 문제였다. 처음에 시간 복잡도를 최대한 줄여보겠다고 한 행과 열에 등장하는 색을 체크하고 수가 적은 행열만 반복하려다가 행과 열을 구분해서 작성하게 되고 오히려 코드가 길어져서 포기했다. 다시 고민해보니 차라리 사방탐색을 하며 경계 체크하고 다르면 바꾸고 해당 요소가 속한 행렬에서 최대 연속 수를 구하는 방식으로 구현했다. 오히려 코드가 명료해졌고 인접한 사탕이 다른 경우에만 바꾸고 시간 복잡도를 고려해 그 사탕이 속한 행렬만 체크하도록 구현했기 때문에 추가로 원래 배열인 경우에도 최대 연속의 수를 구하도록 했다.
이 글을 작성하다 보니 이렇게 풀면 안되었나.. 바꾸고 모든 행렬을 보아야했을까? 라는 생각이 든다. 하지만 내가 바꾼 이 사탕 외에서 최대값이 나온다면.. 그건 원래 배열에서 최대값이 나왔다는 의미니까 원래 배열 한 번만 전체를 순회해서 확인하고 바꾼 사탕이 속한 행렬만 보는 게 최적인 것 같다.
import java.util.Scanner;
public class Main {
public static int n, continuous;
public static char[][] candies;
public static void main(String[] args) {
// 값 입력 받기
input();
// 사방탐색하며 바꿀 수 있는 경우 바꿔서 연속되는 수 구하기
switchJustOne();
System.out.println(continuous);
}
private static void switchJustOne() {
continuous = 0;
checkOriginalArray();
int tempColCon;
int tempRowCon;
int[][] drc = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
for (int d = 0; d < 4; d++) {
int nr = i + drc[d][0];
int nc = j + drc[d][1];
if (nr < 0 || nr >= n || nc < 0 || nc >= n) continue;
if (candies[nr][nc] != candies[i][j]) {
char temp = candies[i][j];
candies[i][j] = candies[nr][nc];
candies[nr][nc] = temp;
// 교환한 채로 체크
tempRowCon = 1;
tempColCon = 1;
for (int k = 1; k < n; k++) {
if (candies[i][k - 1] == candies[i][k]) {
tempRowCon++;
} else {
tempRowCon = 1;
}
if (candies[k - 1][j] == candies[k][j]) {
tempColCon++;
} else {
tempColCon = 1;
}
continuous = Math.max(continuous, Math.max(tempRowCon, tempColCon));
}
// 원상복구
candies[nr][nc] = candies[i][j];
candies[i][j] = temp;
}
}
}
}
}
private static void checkOriginalArray() {
int tempRowCon = 1;
int tempColCon = 1;
for (int i = 0; i < n; i++) {
tempRowCon = 1;
tempColCon = 1;
for (int k = 1; k < n; k++) {
if (candies[i][k - 1] == candies[i][k]) {
tempRowCon++;
} else {
tempRowCon = 1;
}
if (candies[k - 1][i] == candies[k][i]) {
tempColCon++;
} else {
tempColCon = 1;
}
continuous = Math.max(continuous, Math.max(tempRowCon, tempColCon));
}
}
}
private static void input() {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
candies = new char[n][n];
for (int i = 0; i < n; i++) {
candies[i] = sc.next().toCharArray();
}
}
}
강의를 보니 4방이 아닌 오른쪽과 아래 방향만 봐도 반복적으로 교환하는 불필요한 절차는 없어질 것 같다. 또 나는 연속되는 부분을 길이로 변수를 두어 카운트했는데 수 대신 시작되는 타겟 색을 지정해놓고 연속되면 len을 늘리고 바뀌면 다시 해당하는 색을 변경하고 len을 1로 초기화하는 방법으로 구현할 수도 있다.
그리고 예상했던대로 강의에서는 사탕을 바꿀 때마다 배열 전체를 탐색하며 연속되는 최댓값을 구하고 있었다. 사탕을 바꾼 위치와는 관계 없이 다른 곳에서 최댓값이 나올 수도 있다는 점을 가정하고 도는 것이기 때문에 내가 구현한 것처럼 바꾼 곳과 관계되는 행열만 보고 바꾸지 않은 배치에서 가장 긴 연속된 수가 나오는 경우는 한번만 전체 순회를 해주면 될 것 같다. 확인해보니 확실히 내가 푼 방식이 시간이 더 짧게 걸리는 것을 확인할 수 있었다.
'알고리즘 풀이 및 리뷰 > [패캠] 핵심유형 20개로 한 번에 끝내는 알고리즘 코딩테스트 리뷰' 카테고리의 다른 글
| [240219] 알고리즘 리부트 11일차 - 백준 2840 자바 (1) | 2024.02.19 |
|---|---|
| [240218] 알고리즘 리부트 10일차 - 백준 10250, 1730 자바 (0) | 2024.02.18 |
| [240216] 알고리즘 리부트 8일차 - 백준 10448, 11005, 11068 자바 (0) | 2024.02.16 |
| [240215] 알고리즘 리부트 7일차 - 백준 10989, 3273 자바 (0) | 2024.02.15 |
| [240214] 알고리즘 리부트 6일차 - 백준 1236, 10431 자바 (0) | 2024.02.14 |




