| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 그래프
- 스택
- 자바
- 정렬
- 집합
- 백트래킹
- 이분탐색
- 가중치없는그래프
- 알고리즘
- 매개변수 탐색
- 트리
- 자료구조
- dfs
- 해시맵
- MySQL
- Sort
- domain model
- 프로그래머스
- algorithm
- SQL
- git
- Recursion
- 재귀
- microflow
- 멘딕스
- Mendix
- lcap
- 반효경교수님
- Bruteforce
- 완전탐색
- Today
- Total
mondegreen
[240229] 알고리즘 리부트 20일차 - 백준 1931 자바 본문
[240229] 알고리즘 리부트 20일차 - 백준 1931 자바
앙갱 2024. 2. 29. 14:04[Part1-Chapter05-Clip08]
- 백준 1931 회의실 배정

10개월과 1개월 전에 풀었던 문제이고 오늘 다시 풀었다. 사실 이 문제는 끝나는 시간을 기준으로 오름차순 정렬하고 해당 시각이 같을 경우 시작 시각을 비교해서 오름차순으로 정렬하면 되는 문제이다. 이건 회의가 빨리 끝나는 경우 먼저 배정을 해주는 것이 최대한 많은 "수"의 회의를 진행할 수 있기 때문에 이 부분만 알고 있으면 풀어낼 수 있다. 다만 여기서 회의실 미 사용 시간을 최소화하는 경우를 찾으라고 했다면 이 문제 풀이만으로는 부족했을 것이고 여차하면 이렇게 이해를 할 수도 있는 문제였다.
먼저 2차원 배열로 시작시간과 끝나는 시간을 담고 해당 배열을 Sort할 때 Comprator를 이용해 정렬 로직을 구현해주었다. 이후 반복문을 돌면서 이전에 채택된 회의의 끝나는 시각을 다음 회의 시작 가능 시각으로 저장한다. 이 시각과 같거나 늦게 시작하는 경우 그 회의를 채택하고 그 회의의 끝나는 시각을 다시 다음 회의 시작 가능 시각으로 갱신해줌으로써 회의를 계속 선택해나갈 수 있게 한다. 이 때 채택된 회의의 수가 정답이다.
package BaekJoon.sort;
import java.util.Arrays;
import java.util.Comparator;
import java.util.Scanner;
public class BJ1931 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int meetingNum = sc.nextInt();
Integer[][] meetingArr = new Integer[meetingNum][2];
for (int i = 0; i < meetingNum; i++) {
int start = sc.nextInt();
int end = sc.nextInt();
meetingArr[i][0] = start;
meetingArr[i][1] = end;
}
Arrays.sort(meetingArr, new Comparator<Integer[]>() {
@Override
public int compare(Integer[] o1, Integer[] o2) {
if (o1[1] == o2[1]) {
return o1[0] - o2[0];
} else {
return o1[1] - o2[1];
}
}
});
int cnt = 0;
int formerEnd = 0;
for (int i = -1; i < meetingNum - 1; i++) {
//System.out.println("i: "+ i);
if (formerEnd <= meetingArr[i + 1][0]) {
//System.out.println("formerEnd: " + formerEnd);
//System.out.println("다음 시작시간: " + meetingArr[i + 1][0]);
formerEnd = meetingArr[i + 1][1];
cnt++;
}
}
System.out.println(cnt);
}
}
[Part1-Chapter06-Clip02]
- 백준16713 Generic Queries
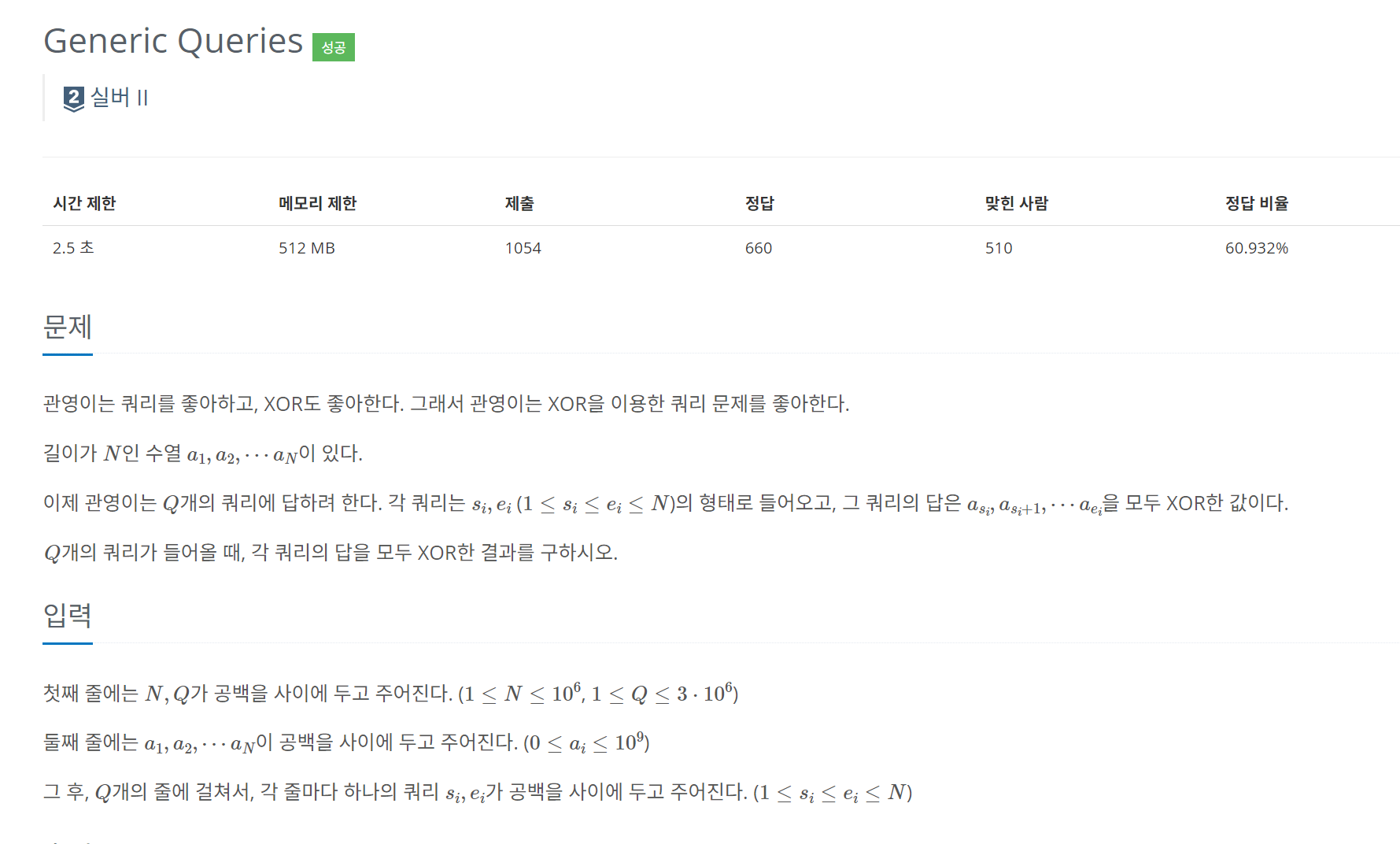
처음에 XOR 연산을 잘못 기억하고(라고 말하지만 제대로 이해하지 못했기 때문이라고 생각한다..) if문으로 처리하다가 ^ 연산처리가 가능하다는 것을 알고 적용해서 처리했다. XOR 연산은 2진수를 기반으로 각 자리가 같을 때 0을 다를 때 1을 반환해 새로운 이진수를 생성하여 반환한다는 것을 잊지 말자. 사실 이 문제의 인덱스를 잘 이해하기 어려워서 풀이 강의를 듣고 추가로 작성하려 한다.
구간합 강의를 듣고 나니 이 문제가 구간합 문제와 동일하다는 것을 알게 되었다. 로직을 직관적으로 이해하려면 백준 11659를 풀어보면 되는데 아래 이미지의 문구가 이 문제는 구간합 문제(여기서는 합 대신 XOR 연산을 함)이라는 것을 보여주는 문구이다. 그래서 아래 코드를 보면 입력을 받음과 동시에 직전 배열의 원소와 XOR 연산을 한다. 또 쿼리에 대해 시작점과 끝점을 주고 시작점 직전의 원소와 끝점의 원소를 XOR 연산 해주는데 이렇게 처리하면 시작점 이전까지의 누적된 XOR 결과값을 제외할 수 있기 때문이다.
XOR 연산에 익숙하지 않아서 손으로 직접 예시들을 작성해보았다. 구간에 해당하는 각 배열의 원소를 연산해보고 풀이와 같이 시작점 직전의 원소 값과 끝점의 원소값을 XOR 해보니 값이 같았다. 이는 XOR 연산이 값이 다른 경우 단순히 1과 0을 치환하는 연산임에 따라 (같다면 유지, 즉, 복원작업이 가능) 시작점 직전까지의 원소를 연산에 포함시키지 않기 위해서는 직전의 원소와 끝점에 대해 XOR 연산을 해주면 가능했던 것이다.
이렇게 누적 연산이 가능하려면 위에서 말한 복원작업이 가능해야 하는데 이렇게 가능한 연산은 합, 곱, XOR 연산(당연 빼기와 나눗셈과 가능)이 있다. (최대값, 최소값, 최대공약수 등의 연산은 불가)
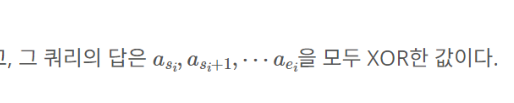
package BaekJoon.prefixSum;
import java.util.Arrays;
import java.util.Scanner;
public class BJ16713_1 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int arrLen = sc.nextInt();
int queryLen = sc.nextInt();
int[] arr = new int[arrLen + 1];
for (int i = 0; i < arrLen; i++) {
arr[i + 1] = arr[i] ^ sc.nextInt();
}
System.out.println(Arrays.toString(arr));
int result = 0;
for (int i = 0; i < queryLen; i++) {
int first = sc.nextInt();
int second = sc.nextInt();
result = result ^ (arr[first-1] ^ arr[second]);
//System.out.println("result: " + result);
}
System.out.println(result);
}
}'알고리즘 풀이 및 리뷰 > [패캠] 핵심유형 20개로 한 번에 끝내는 알고리즘 코딩테스트 리뷰' 카테고리의 다른 글
| [240305] 알고리즘 리부트 24일차 - 백준 17232 자바 (1) | 2024.03.06 |
|---|---|
| [240301] 알고리즘 리부트 21일차 - 백준 11659, 11660, 19951 자바 (0) | 2024.03.01 |
| [240226] 알고리즘 리부트 17일차 - 백준 2910 자바 (0) | 2024.02.25 |
| [240225] 알고리즘 리부트 16일차 - 백준 18870 자바 (1) | 2024.02.25 |
| [240224] 알고리즘 리부트 15일차 - 백준 10814, 1302 자바 (1) | 2024.02.24 |




